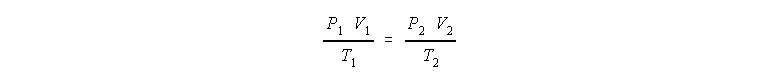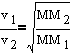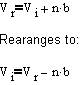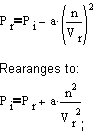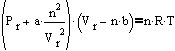Chapter 5 Lecture Outline

5.1 Breathing: Putting Pressure to Work

5.2 Pressure: The Result of Molecular Collisions

  1. Units
    1. Pressure (what it is and units)
      2. Pa (N/m2) 101325 Pa = 1 atm
      bar (105 Pa) 1.01325 bar = 1 atm
      torr and mmHg (133.322 Pa) 760 torr = 1 atm
      atmosphere (101325 Pa)
      PSI (6894.76 Pa) 14.7 PSI = 1 atm

    2. Temperature (Use Kelvin Scale, 273.15)

    3. Volume
      4. Unit Conversion to Liter Conversion to m3
      m3 103 liter 1 m3
      cm3 (ml) 10-3 liter 10-6 m3
      liter (dm3) 1 liter 10-3 m3
      ft3 35.323 liter 0.03532 m3
      in3 0.01639 liter 1.639x10-5 m3

  2. Standard Temperature and Pressure (STP)
    1. 1 bar (105 Pa), previously 1 atm
    2. 0 °C

5.3 The SimpleGas Laws: Boyle's Law, Charles's Law, and Avogadro's Law

  1. Introduce concept of an ideal gas
    1. No volume
    2. No interaction
    3. Discuss behavior of ideal gas

  2. Ideal Gas Behaviors. Gas Law Spreadsheet (123, Excel)

    1. Boyle's Law (PV = CB)
      1. Derive relationship from ideal gas "concept with picture on board
      2. Animation from ( Internet© Saunders, 1997)
      3. Graph relationship
      4. Write equation for graph
      5. Work a problem.

    2. P/T = C
      1. Derive relationship from ideal gas "concept with picture on board
      2. Animation from ( Internet© Saunders, 1997)
      3. Graph relationship
      4. Write equation for graph
      5. Work a problem.

    3. Charles Law (V/T = CC)
      1. Derive relationship from ideal gas "concept with picture on board
      2. Graph relationship
      3. Write equation for graph
      4. Work a problem.

    4. Combine above equations to get (PV)/T = C

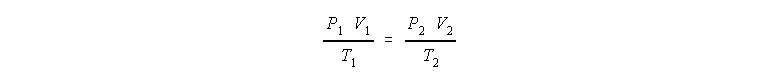
    5. Practice Problems.

  3. P/n = C
    1. Derive relationship from ideal gas "concept with picture on board
    2. Animation from ( Internet© Saunders, 1997)
    3. Graph relationship
    4. Write equation for graph
    5. Work a problem.

5.4 The Ideal Gas Law

  1. Gas data for 1 gram at STP. Calculate the molar volume
    1. H2 11.1 L
    2. He 5.57 L
    3. N2 0.800 L
    4. Cl2 0.316 L

  2. Relate molar volume to combined gas law and derive ideal gas law
    1. PV = nRT
    2. Units for R
      1. Calculate R from above data
      2. Convert R to SI units (Note: Pa = N/m2 and J = Nm)
    3. How many moles of gas in the sampling balloon above?

  3. Work a problem.

5.5 Applications of the Ideal Gas Law: Molar Volume, Density and Molar Mass of a Gas

5.6 Mixtures of Gases and Partial Pressures

  1. Dalton's Law of Partial pressure
    1. Ptotal = P1 + P2 + P3 + ...
    2. Ptotal V = (n1 + n2 + n3 + ...) RT

  2. Problem

5.7 Gases in Chemical Reactions: Stoichiometry Revisited

5.8 Kinetic Molecular Theory: A Model for Gases

  1. What is an ideal gas

  2. elastic collisions

  3. Boltzman Plots ( Internet© Saunders, 1997)

  4. KEavg proportional to T

  5. KE = 1/2 mv2

  6. For two different gases

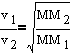
5.9 Mean Free Path, Diffusion , and Effusion of Gases

5.10 Real Gases: The Effects of Size and Intermolecular Forces

  1. Non Ideal Behaviors
    1. Volume of gas particles (Overhead)
    2. Interaction of gas molecules (overhead)
  2. Derive van der walls equation
    1. Start with the ideal gas law where Pi and Vi are the "ideal" pressure and volume:

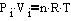
    2. The "real" volume (Vr) is the ideal volume plus the volume of the gas molecules (n*b), where n is the number of moles and b is the volume of one mole of gas molecules. That is the molecules, not the space that contains the molecules.

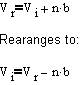
    3. The "real" pressure (Pr) is the ideal pressure minus a term that describes how the gas molecules stick together. This sticking together reduces the apparent pressure. It is possible to develop this equiation from "first principles", but we will leave that exercise for when you take physical chemistry.

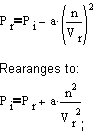
    4. Now these new expressions for the ideal pressure and the ideal volume may be substituted into the ideal gas law to give:

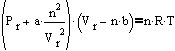
    5. Which is the Van der Walls equation.

  3. Work an problem.

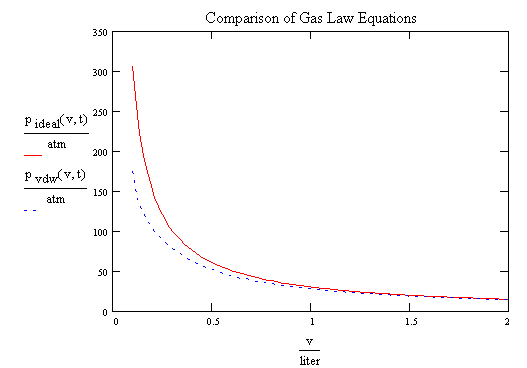
  4. Comparison of ideal gas and Van der Walls gas from Mathcad
    1. Helium at 25 C (pressure vs volume)

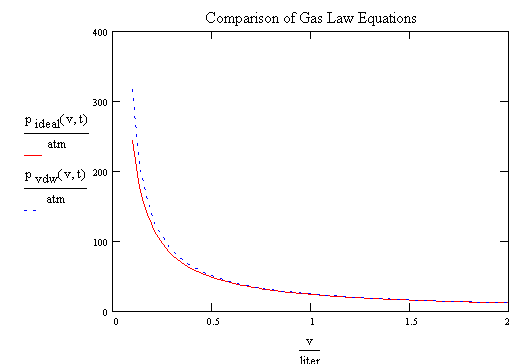
    2. CO2 at 25 C

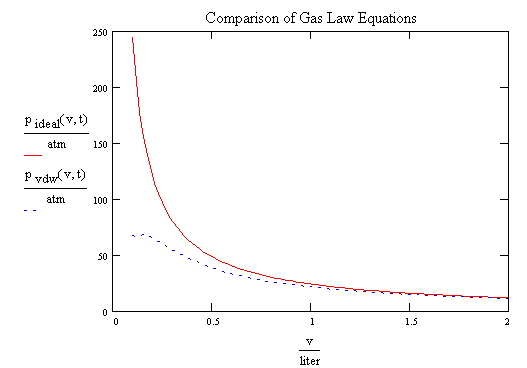
    3. CO2 at 100 C

This page is maintained by
Scott Van Bramer
Department of Chemistry
Widener University
Chester, PA 19013

Please send any comments, corrections, or suggestions to svanbram@science.widener.edu.

This page has been accessed times since 5/30/97.
Last Updated Friday, May 25, 2001 1:59:43 PM